Fresh Page
"Software is invisible and unvisualizable. Geometric abstractions are powerful tools. The floor plan of a building helps both architect and client evaluate spaces, traffic flows, views. Contradictions become obvious, omissions can be caught. Scale drawings of mechanical parts and stick-figure models of molecules, although abstractions, serve the same purpose. A geometric reality is captured in a geometric abstraction.
The reality of software is not inherently embedded in space. Hence it has no ready geometric representation in the way that land has maps, silicon chips have diagrams, computers have connectivity schematics. As soon as we attempt to diagram software structure, we find it to constitute not one, but several, general directed graphs, superimposed one upon another. The several graphs may represent the flow of control, the flow of data, patterns of dependency, time sequence, name-space relationships. These are usually not even planar, much less hierarchical. Indeed, one of the ways of establishing conceptual control over such structure is to enforce link cutting until one or more of the graphs becomes hierarchical.
In spite of progress in restricting and simplifying the structures of software, they remain inherently unvisualizable, thus depriving the mind of some of its most powerful conceptual tools. This lack not only impedes the process of design within one mind, it severely hinders communication among minds."
— Frederick P. Brooks, The Mythical Man-Month, 1975
It is hard to say how infuential these ideas have been. But considering that visualization discussions have, almost exclusively, been reserved for data and the so called visual languages have been a variation on clumsy flow charts; Most people must feel a similar resignation.
In any case, it is worth asking if programs with various layers of complexity can be made to appeal to our visual and spatial capacities. The importance of which is probably parallel to majority volume of brain regions and share of neural processing power.
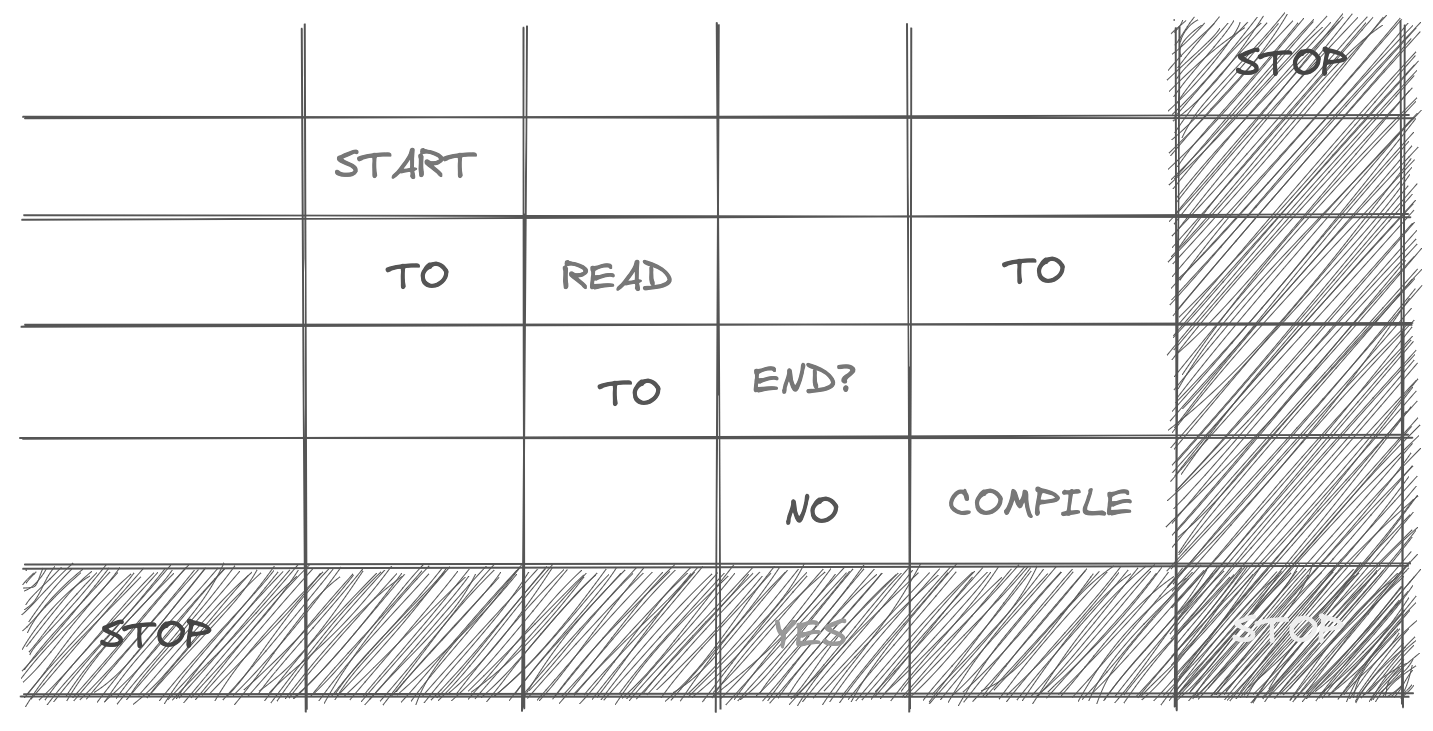
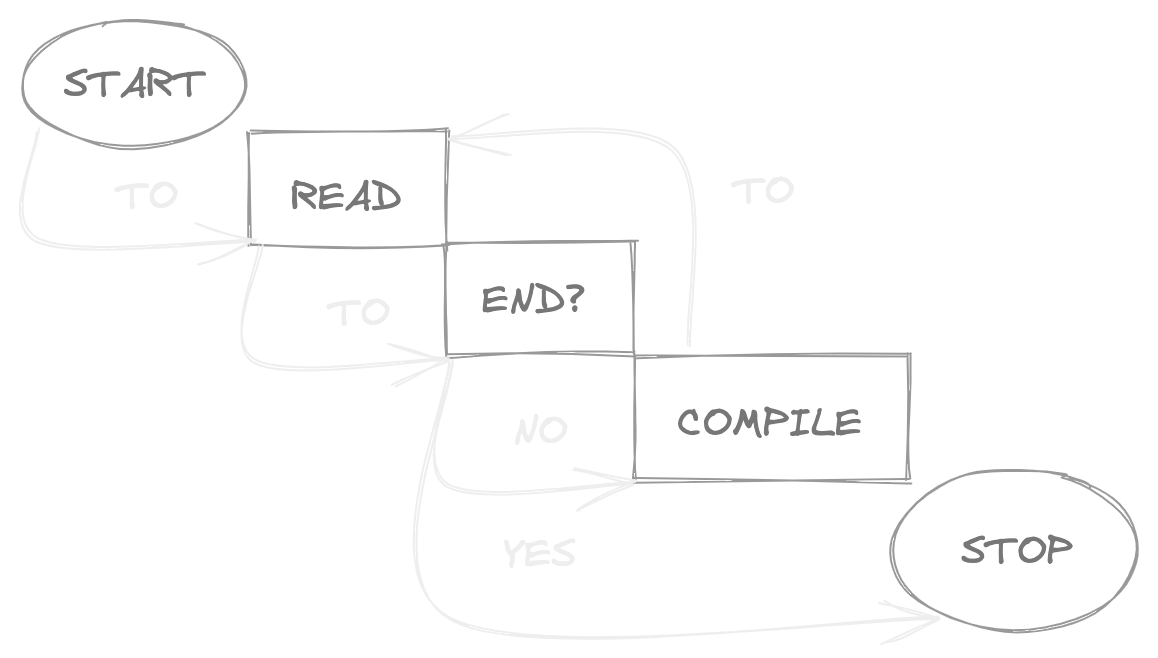
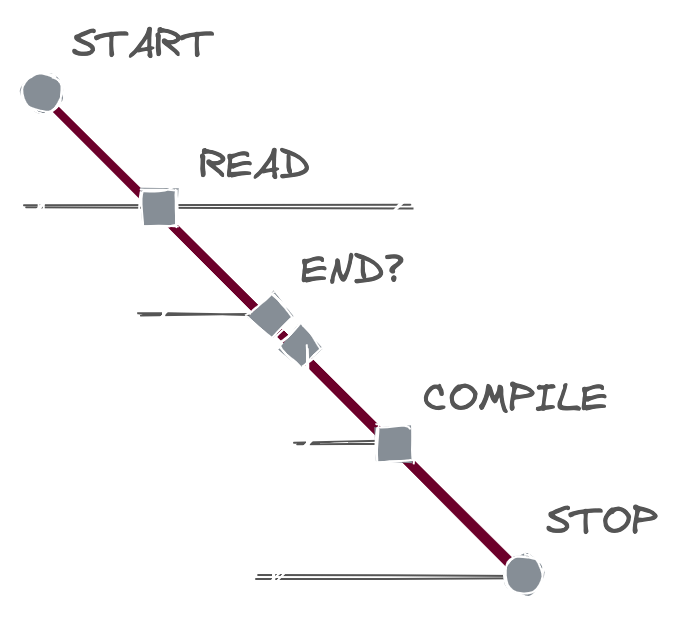
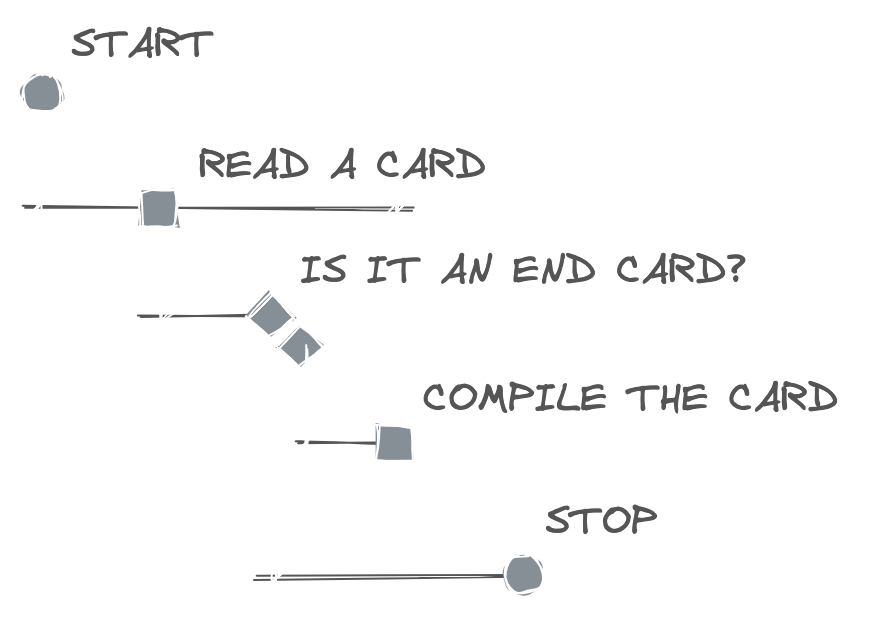
Above is a sample flowchart for a simple algorithm with conditionals and loops. It is good for an overview but quickly turns into a mess with some details. Below is the same graph in matrix representation. Each column is reserved for outgoing links, rows for incoming links.
Leaving valuable space empty makes it impossible to use in physical media. But, requiring very litle for rendering, it deserves further attention for interactive programs that can refresh the finite screen.
1. The first row will be left empty, meaning no incoming links.
2. The final column with no outgoing links will also be left empty.
3. Since the loops manifest in multiple nodes, the diagonal will also be empty.
The diagonal cells, being at the intersection of a row and column, can serve special duty.
1-5. Node labels can be placed on these cells and not be duplicated at the headers.
6. The new matrix.
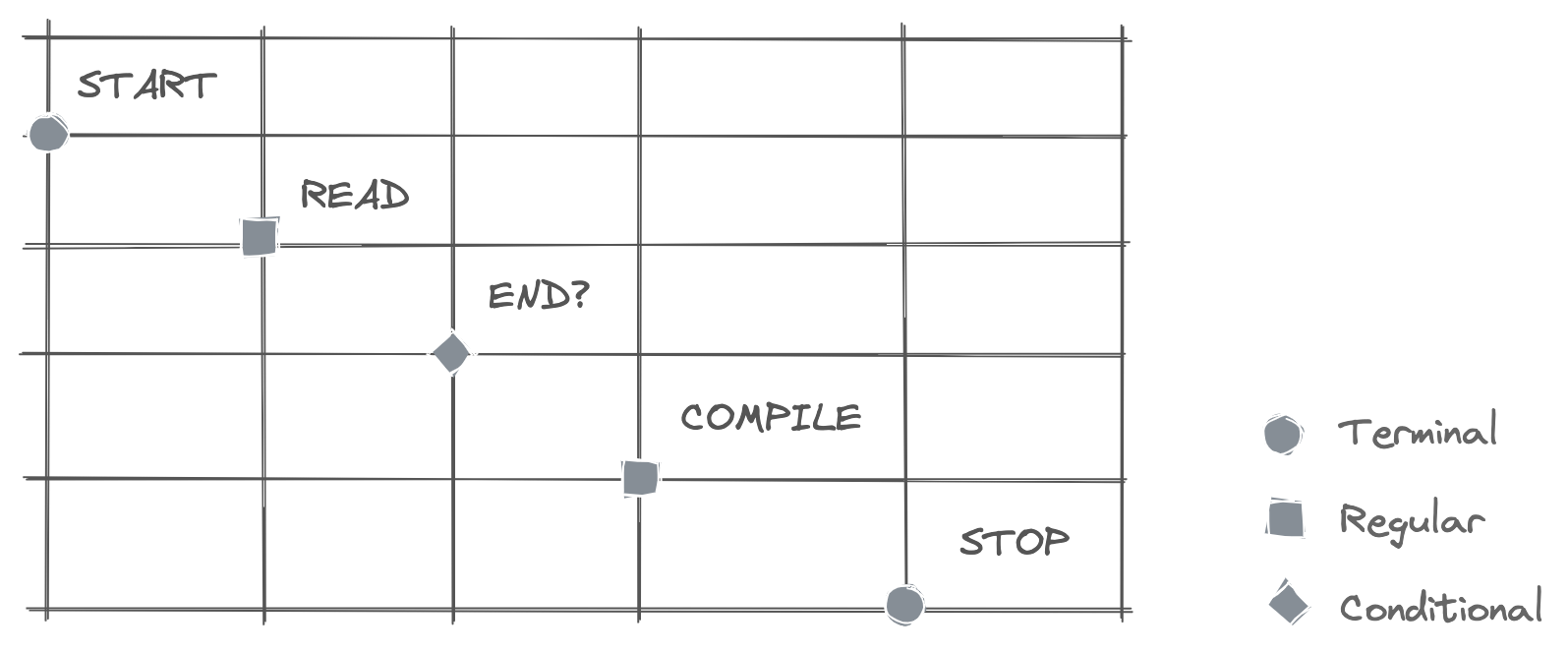
Now that the node labels are localized, the matrix appears like a restriction on the positioning of nodes and shape of connections.
Visual distinctions will bring the two representations together.
1. Taking the table again.
2. Symbols can convey the roles of nodes.
3. Outgoing and incoming lines can be differentiated with brightness.
4. Lines beyond the connection corner can be trimmed.
5. Corners become the anchor for all information.
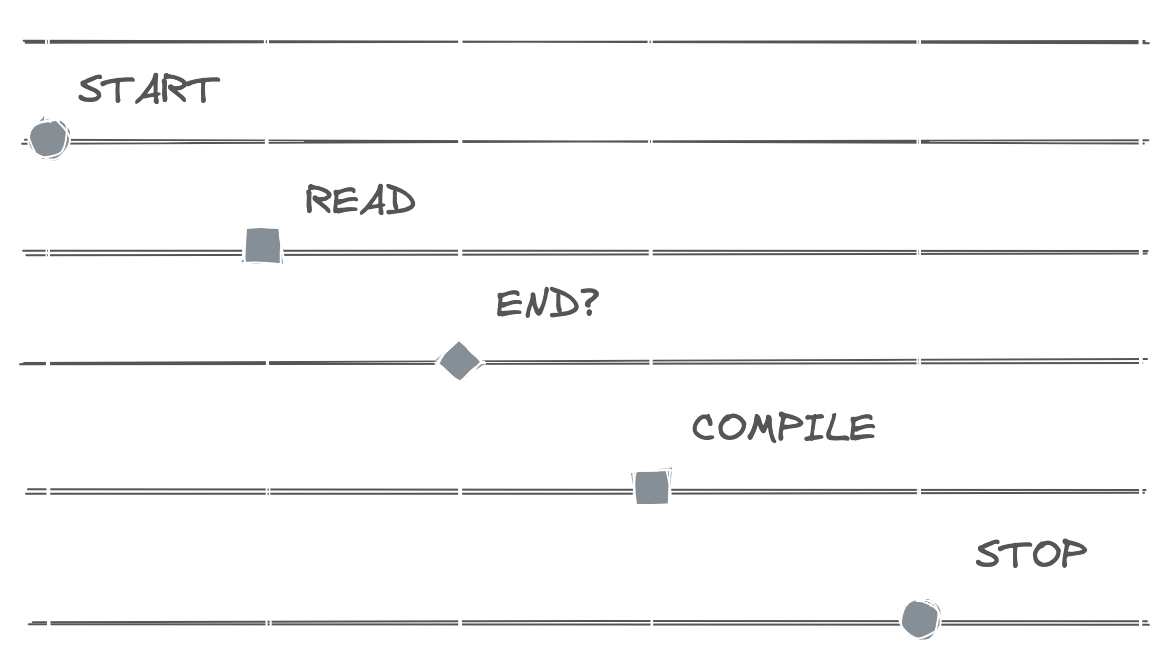
There is some waste in the space utilization. And there is some benefit in rapid redrawing and navigation on a two dimensional discrete space. I feel on track for an alternate presentation.
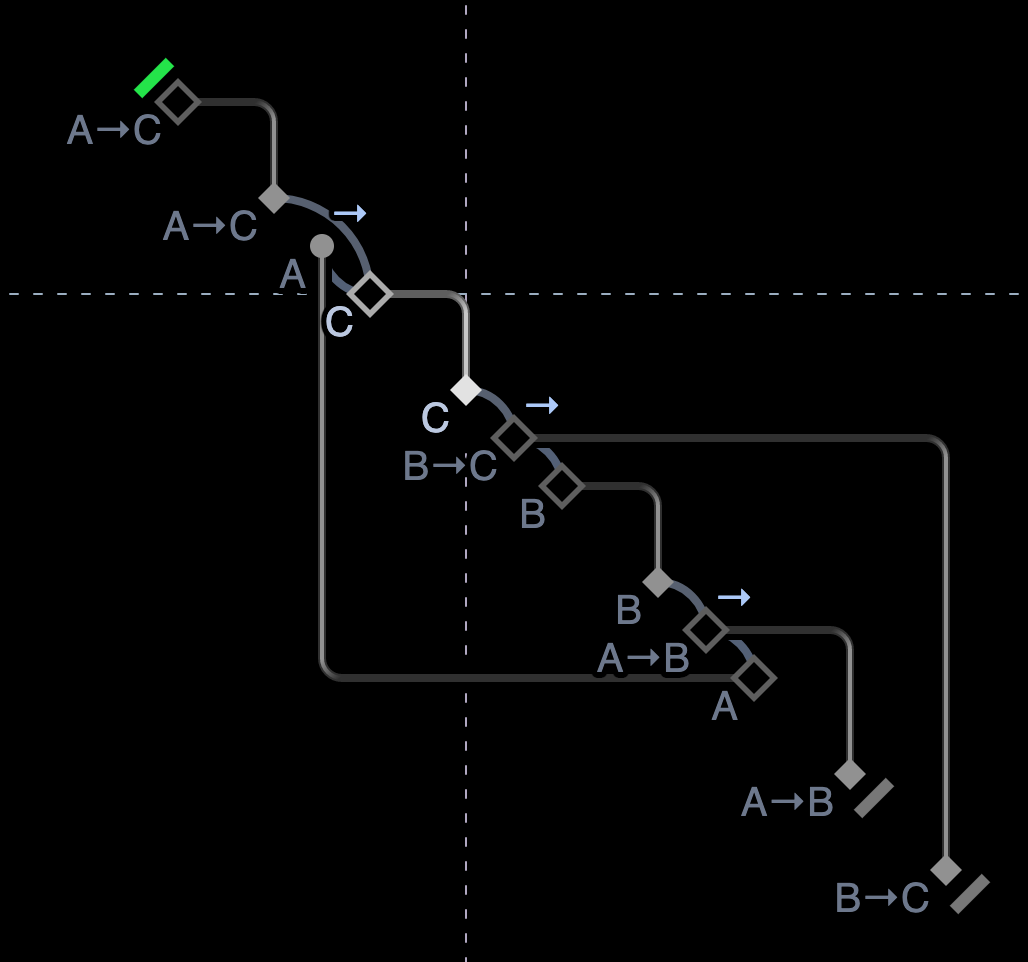
Now, the restrictions on the layout can be utilized to convey further distinctions. As an example of the details that can be incorporated in to the presentation: multiple outgoing connections will be differentiated at the source.
1. From the step before.
2. Connection labels are no longer scattered on the matrix. It is not necessary to vary the width of columns.
3. The nodes can all be positioned along a straight line. Connection lines as simple guides to corners are left on the background.
4. Longer labels can extend in the row.
This is my static introduction to dynamic graph presentation with a balanced emphasis on two aspects of machine presence: visualization and manipulation of structure.
One interactive experiment is based on proof graphs of incredible.pm. Including blocks with multiple input and output ports.
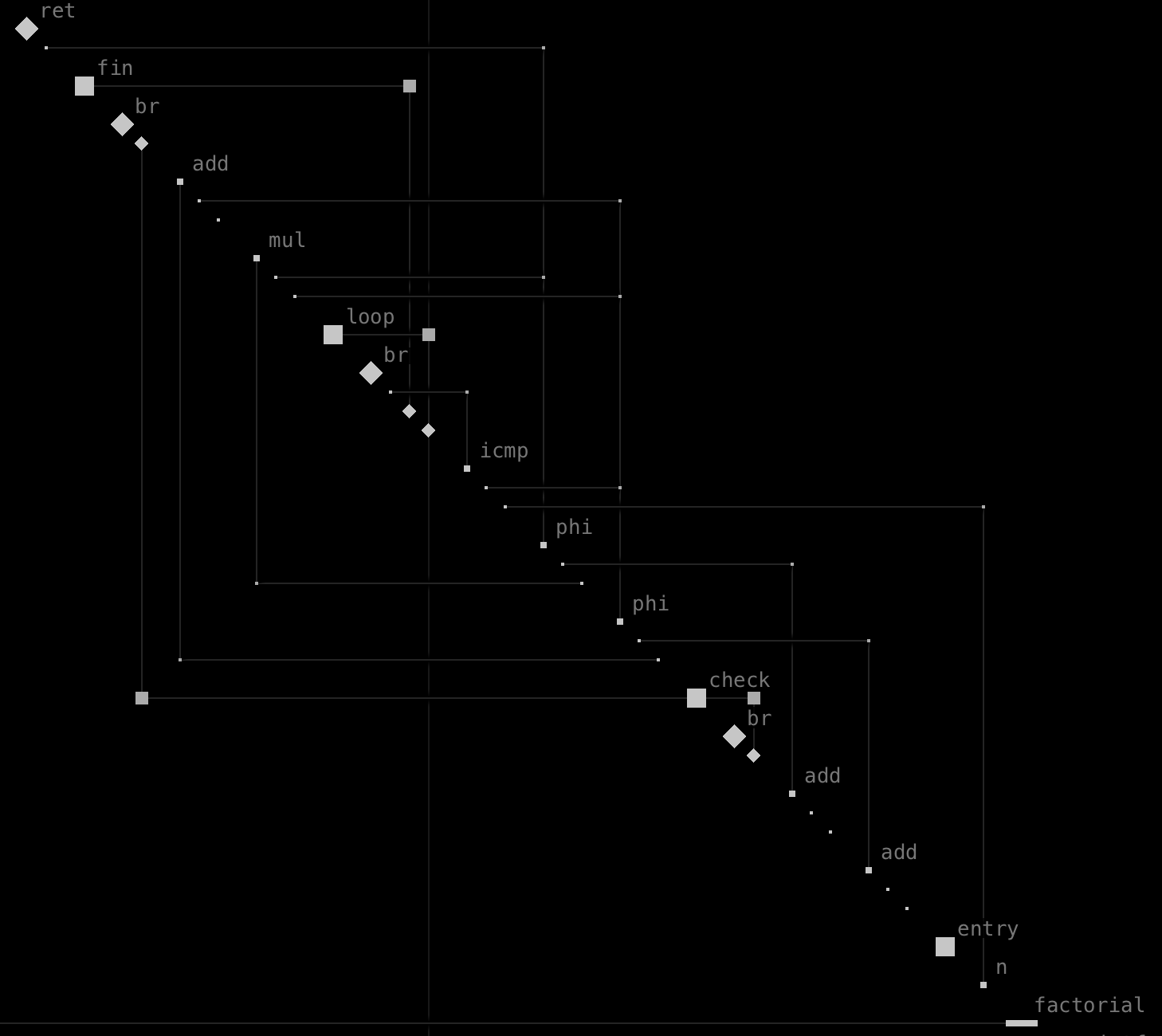
The first experiment was on presenting LLVM IR: rw. Below is an updated view on it. It includes a function with multiple blocks, each of which contains multiple instructions having multiple arguments. The various layers of detail is differentiated by the size and shape of the symbols.
Initial motivation for this was an article: Magic Ink by Bret Victor. Which can be summarized as: Today's software can be made much better just by relying on traditional graphic design. It could have just as easily concluded: Digital screens are mostly used as a bad imitation of paper. But somehow that conclusion is obstructed by the title.
After a few experiments, I was convinced that screens are really under-utilized and went to work on read.machinepresence.com. At the time, it seemed like all software was an extension of bureacracies and i needed to stand far back for a fresh perspeective.
As to the goal, it can be stated as a hope to make graph editing as straightforward as text editing. So that programming languages, which is the only proper interface to programmable machines, can find new graound and open up new possibilities.
In any case, graphs are the most flexible structure used in models and designs. It is fun to care for them. And gratitude for your attention.
